Introduction¶

Learning outcomes¶

• Understand hydrostatic forces on inclined surfaces
• Learn about and how to use the concept of the pressure prism
• Understand hydrostatic forces on curved surfaces
• Learn about buoyancy and how heavy things like ships float

Hydrostatic force on plane surfaces¶

Consider a large rectangular water tank such as a swimming pool. We've already looked at the effect of depth on pressure but now we want to look as the forces exerted by the fluid on its surroundings.

We want to understand the fores the volume of fluid exerts on the bottom and side walls.

Which we can simplify this example into a 2D problem as shown below. Note that the inverted triangle represents the level of the free surface which is subject to atmospheric pressure. We can consider it analogous to an electrical ground.

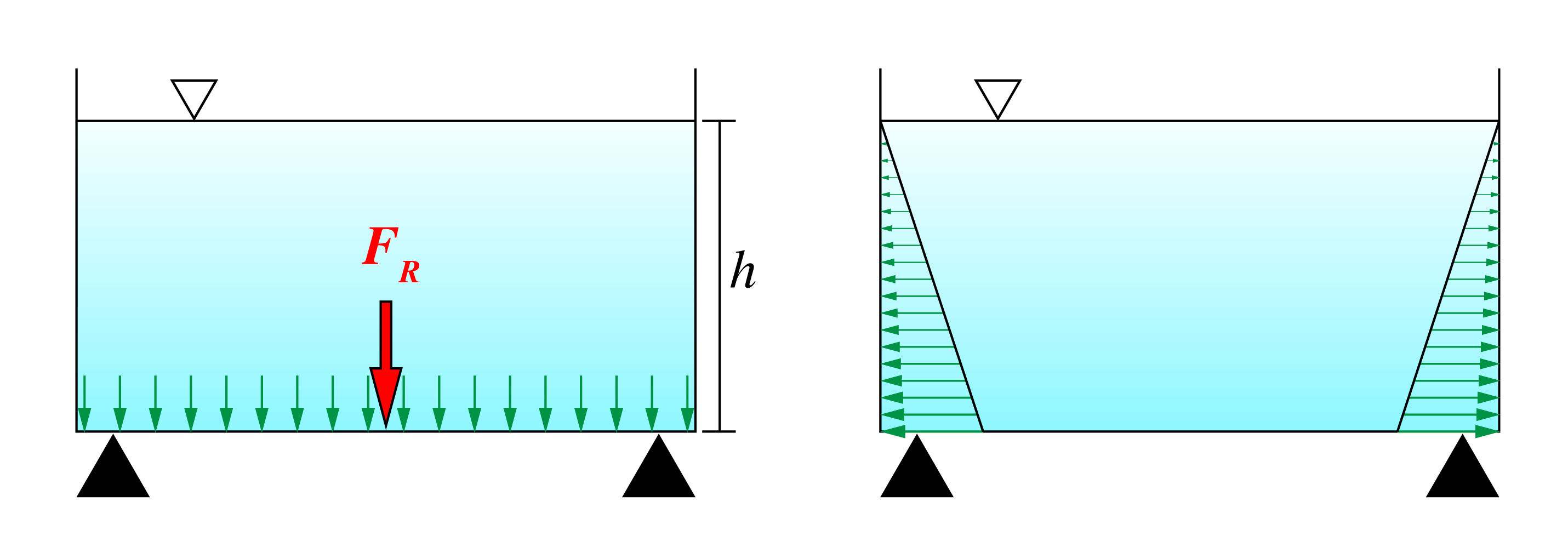
For the forces acting on the bottom surface (area $A$) we can simply integrate over the pressure distribution on that surface.

\begin{equation} F_R = \int_A p dA = \gamma h A \end{equation}

However on the side walls the calculation is more complicated since the the pressure distribution on the side walls increases with depth. As shown above it is zero at the surface and increases to some maximum value. This is an important engineering problem as it determines the structural strength required in many engineering areas such as hydroelectric power generation, marine engineering and civil engineering.

Hydrostatic force on an arbitrarily inclined surface¶

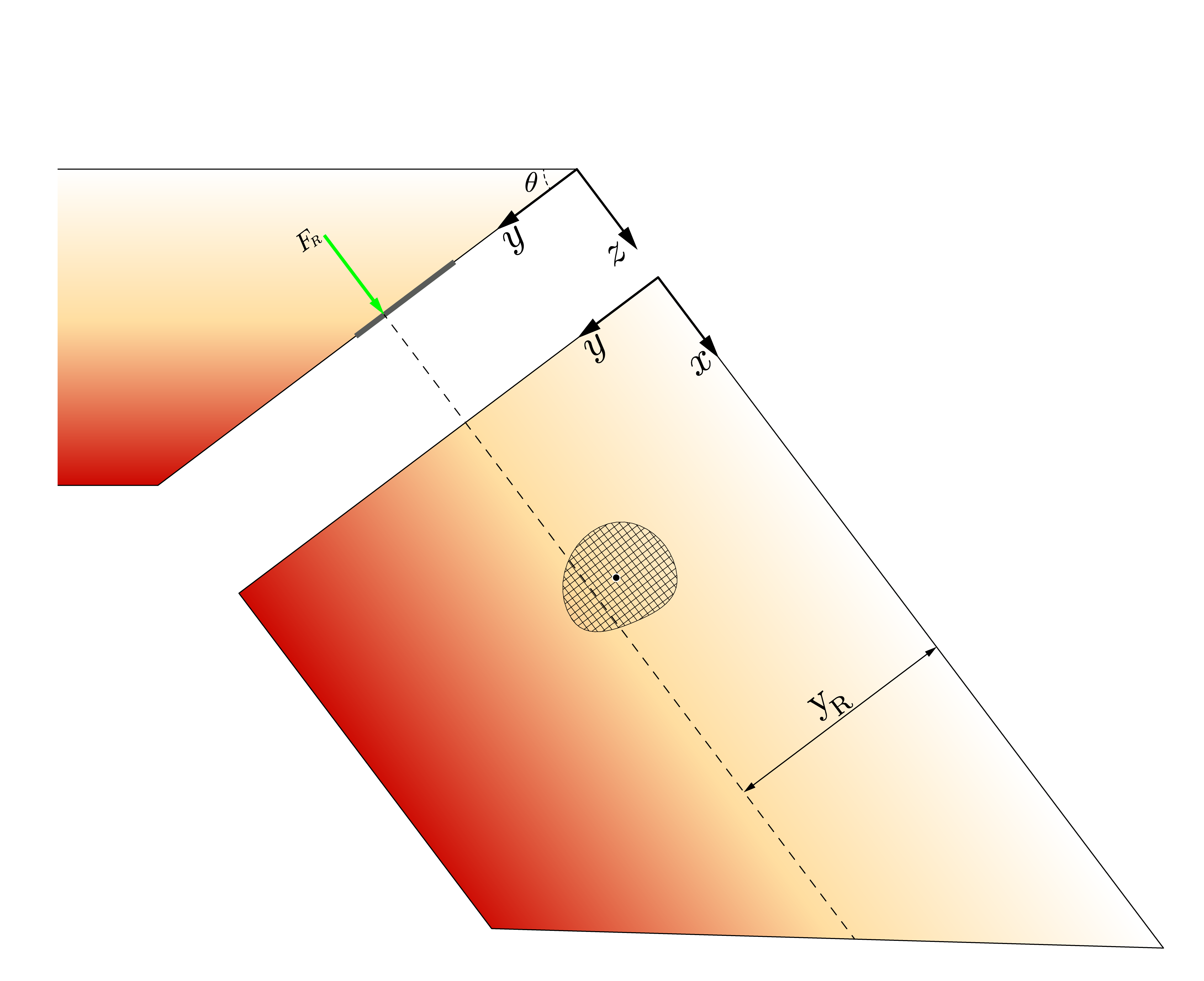
In order to determine the force acting on a vertical place surface, as in the case of the swimming pool, it is better to generalise the problem and consider any surface at some angle on inclination $\theta$. The 3D model below shows such a generalised shape. A coordinate system $(x, y, z)$ is inclined at the angle $\theta$ along the wall of interest.

View in AR

Taking a view of the inclined side wall we can take an arbitrary area A as shown:¶

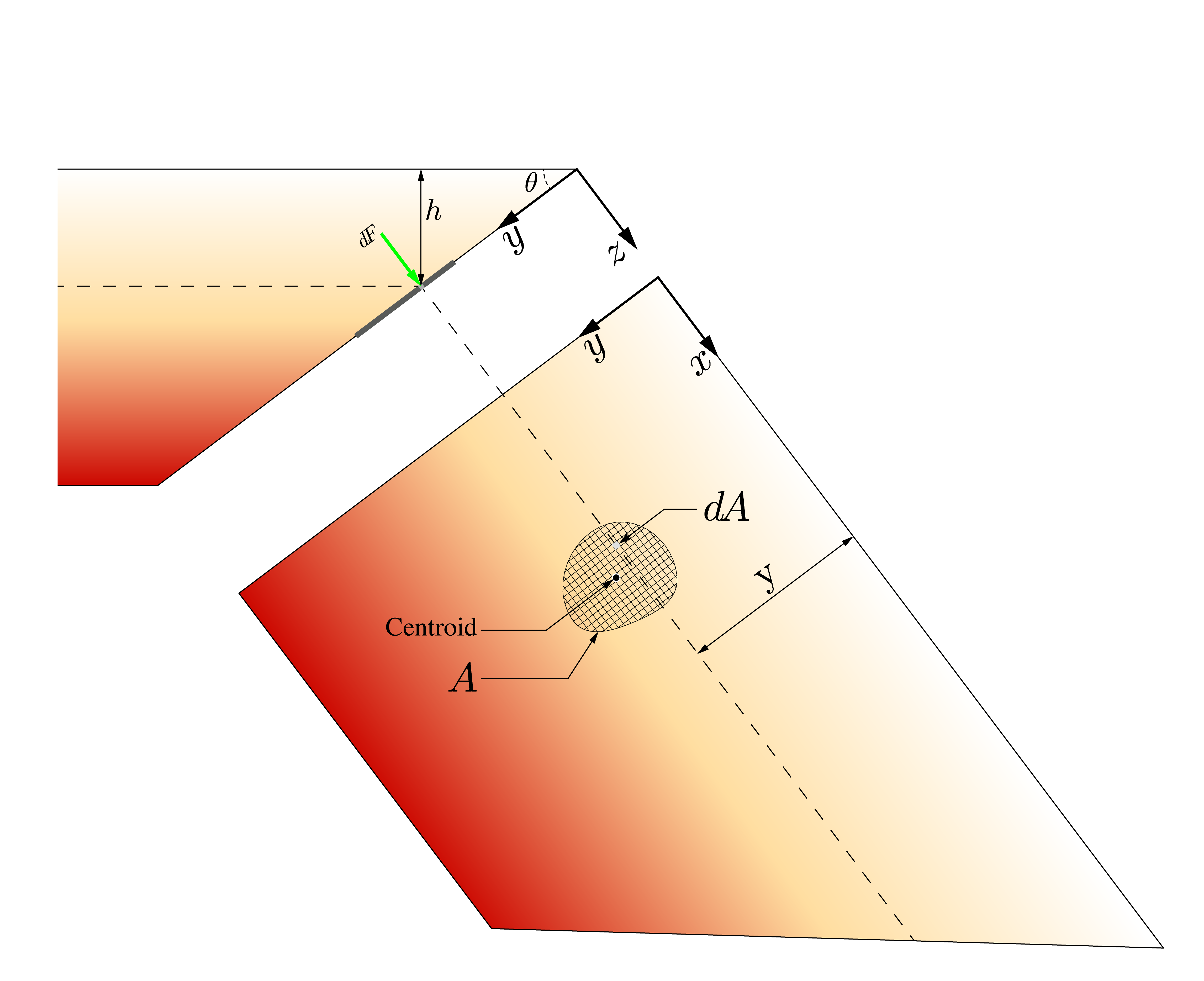
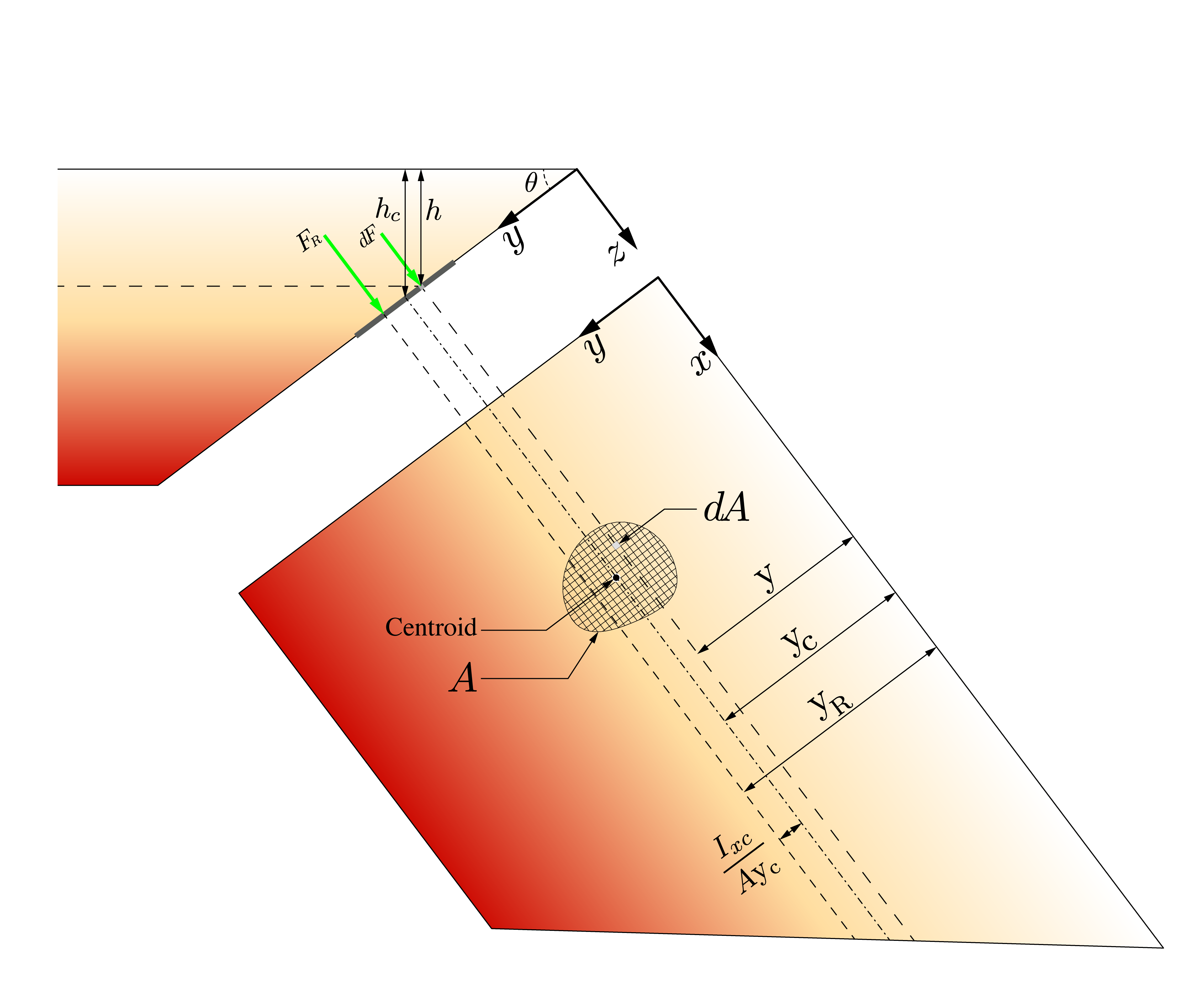
If we consider an infinitesimal element of area $dA$ residing in the arbitrary area $A$ on the inclined wall, we can use what we already know to compute the hydrostatic pressure $dp$ at the depth $h$.

\begin{align} dp = \rho g h = \gamma h \end{align}

The force $dF$ acting on the element is then:

\begin{align} dF = \gamma h~{d\!A} = \gamma [\mathrm{y}\sin{\theta}]~{d\!A} \end{align}

Integrating over the entirety of area $A$ allows us to compute the resultant force from the forces acting on each element of $A$.

\begin{align} F_R = \gamma \sin(\theta) \int_A \mathrm{y}~{d\!A} \end{align}

You may recognise that the integral takes the form of the First Moment of Area:

\begin{align} \int_A \mathrm{y}~{d\!A} = \mathrm{y_c} A \end{align}

Which gives us:

\begin{align} F_R = \gamma \sin(\theta)~\mathrm{y_c} A \end{align}

Where $\mathrm{y_c}$ is the position of the centroid of $A$ along the local $y$-axis.

We can write this in terms of $h_c$:

However you will notice in the diagram below that the force $F_R$ does not pass through the centroid located at a depth $h_c$. This makes intuitive sense. The lower elements in area $A$ will experience greater force $dF$ than those closer to the surface. Therefore the force will be distributed towards the bottom and the resultant of that force will therefore be lower than the centroid.

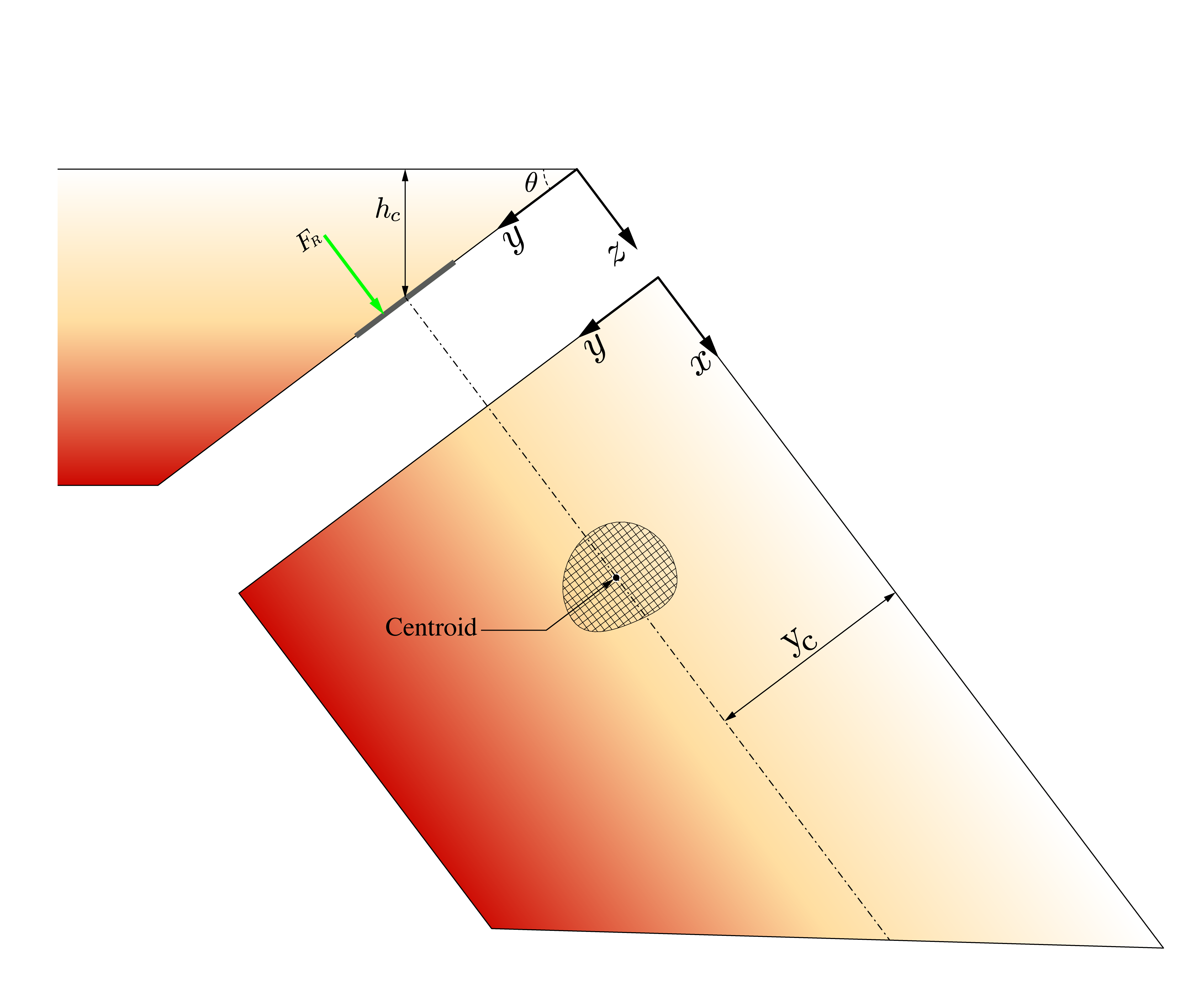
Next we need to compute the distance $\mathrm{y_R}$ the distance at which the force $F_R$ acts. To do this we take moments about $x$ for every force $dF$ acting at every distance $\mathrm{y}$ for every infinitesimal element in area $A$.

\begin{align} F_R \mathrm{y_R} = \int_A \mathrm{y}~{d\!F} = \gamma \sin{\theta} \int_A \mathrm{y}^2~{d\!A} \end{align}

Since $F_R = \gamma\sin{\theta}~\mathrm{y_c} A$ we can substitute and obtain:

\begin{align} \mathrm{y_R} = \frac{1}{A\mathrm{y_c}} \int_A \mathrm{y}^2~{d\!A} \end{align}

The second moment of area has the form:

\begin{align} I_x = \int_A \mathrm{y^2}~{d\!A} \end{align}

therefore:

\begin{align} \mathrm{y_R} = \frac{I_x}{A\mathrm{y_c}} \end{align}

We can employ the parallel-axis theorem to determine the second moment of area about $\mathrm{y_R}$ relative to that around the centroid.

\begin{align} I_x = I_{xc} + A\mathrm{y^2_c} \end{align}

which yields:

We have already seen the denominator, $A\mathrm{y_c}$; it is the first moment of area and the numerator $I_{xc}$ is the second moment of area about the centroid, both of which have positive values. Therefore the distance $\frac{I_{xc}}{A\mathrm{y_c}} > 0$ which means that $\mathrm{y_R}$ is always lower than $\mathrm{y_c}$.

Combining the above figures:

Location of $F_R$ in the $x$ direction¶

To locate the point which $F_R$ acts in the $x$-direction we take moments about the $y$-axis.

\begin{align} F_R \mathrm{x_R} = \int_A \mathrm{x}~{d\!F} = \int_A \gamma \sin{\theta}~\mathrm{xy}~{d\!A} \end{align}

Since $F_R = \gamma\sin{\theta}~\mathrm{y_c} A$ we can again substitute and obtain:

\begin{align} \mathrm{x_R} = \frac{\int_A \mathrm{xy}~{d\!A}}{A\mathrm{y_c}} = \frac{I_{xy}}{A\mathrm{y_c}} \end{align}

Once more invoking the parallel-axis theorem

\begin{align} I_{xy} = I_{xyc} + A\mathrm{x_c y_c} \end{align}

we obtain:

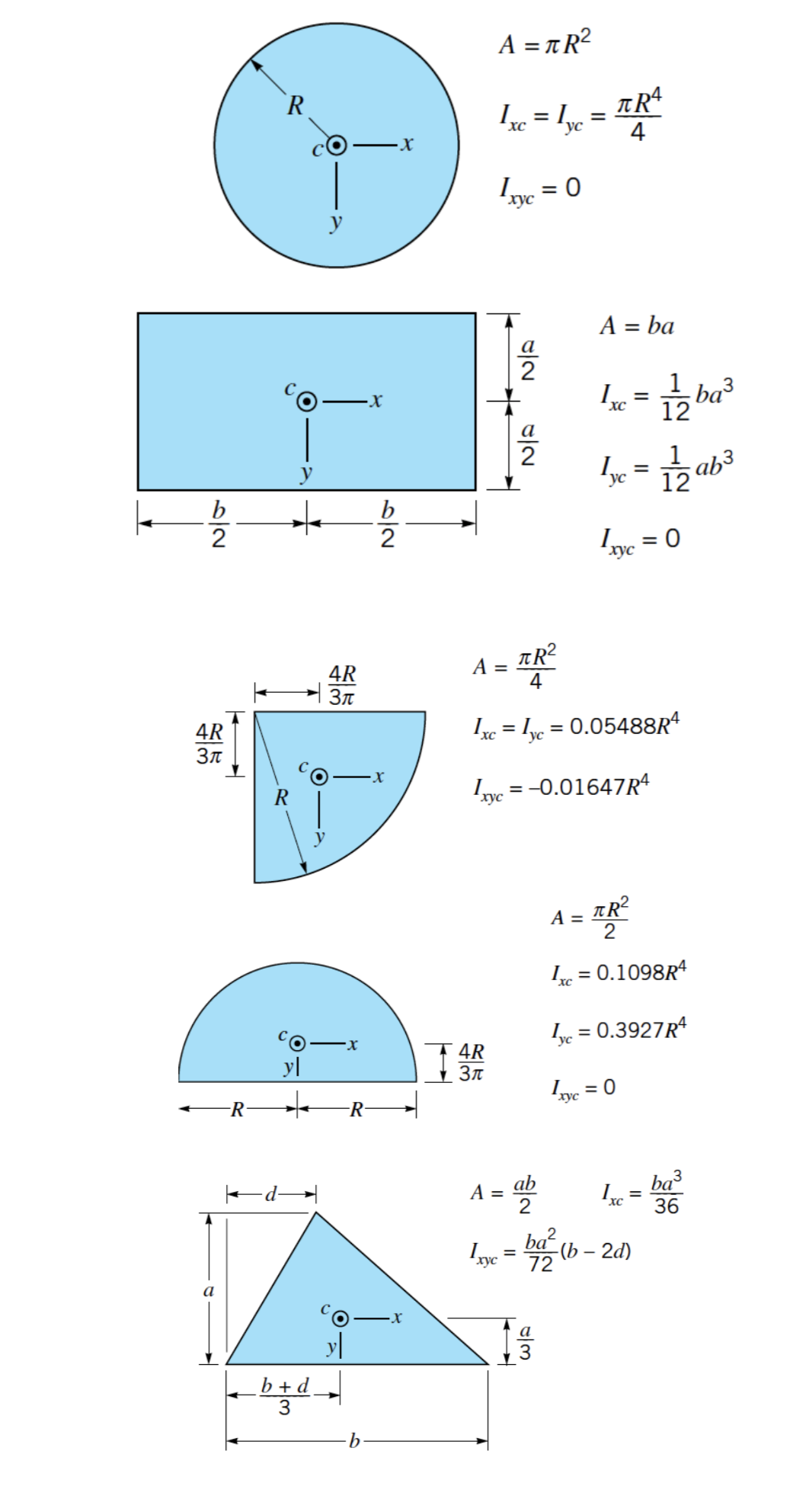
Munsen et al.[1] provides a useful reference of a the geometric properties for a number of common shapes. A version of it is reproduced here and will also be available in the final exam.

Example¶

This example is taken from Munsen et al. [1].

A $4m$ diameter circular gate is located in the inclined wall of a large reservoir containing water. The gate is mounted on a shaft along its horizontal diameter.

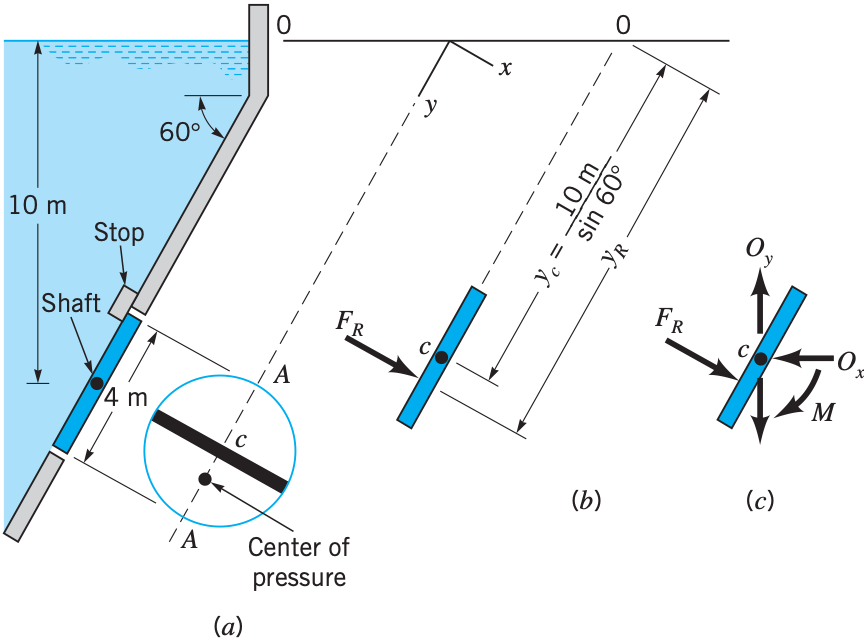
For a water depth of $10m$ above the shaft determine:

1. the magnitude and location of the resultant force exerted on the gate by the water, and
2. the moment that would have to be applied to the shaft to open the gate.

$\gamma =9.8kN m^3$

Part 1¶

The resultant force, as we have seen above, may be determined from

\begin{equation*} F_R = \gamma h_c A = (9800)(10)\frac{\pi 4^2}{4} = 1.23\times 10^6~N \end{equation*}

To determine the centre of pressure we once again follow the above derivation. We have shown:

\begin{equation*} \mathrm{y_R} = \frac{I_{xc}}{A\mathrm{y_c}} + \mathrm{y_c} \end{equation*}

We need $I_{xc}$ and $y_c$ to compute $\mathrm{y_R}$. For a circle we now know

\begin{equation*} I_{xc} = \frac{\pi R^4}{4} = \frac{\pi 2^4}{4} = 12.57m^4 \end{equation*}

Next we can calculate the distance along the angled wall

\begin{equation*} y_c = \frac{h_c}{\sin{\theta}} = \frac{10}{\sin{60^\circ}} = 11.55m \end{equation*}

Now can can solve part 1.

\begin{equation*} \mathrm{y_R} = \frac{I_{xc}}{A\mathrm{y_c}} + \mathrm{y_c} = \frac{12.57}{(12.57)(11.55)} + 11.55 = 0.0866+11.55 = 11.64m \end{equation*}

Part 2¶

The moment $M$ required to open the gate may be determined by taking moments about the gate shaft. The distance $(\mathrm{y_R} − y_c )$ is where the force $F_R$ acts relative to the shaft.

\begin{align*} M &= F_R (\mathrm{y_R} − y_c )\\ &= (1.23\times 10^6)(0.0866 ) = 1.07\times 10^5 Nm \end{align*}

The Pressure Prism — A graphical approach¶

The pressure prism is a graphical method to determine the hydrostatic force acting on a plane vertical area. You may find it more intuitive than the more general but mathematical method above.

To obtain the pressure prism we will use the previous approach and make some general observations.

To determine the magnitude of the force acting on the vertical wall we simply compute the pressure at the location of $h_c$, the centroid of the surface, which for a vertical wall is halfway down the wall.

Which is simply the average pressure on the wall times the area.

\begin{align} F_R = p_{average} A = \left(\frac{\gamma h}{2}\right) \left( b h \right) = \left(\frac{\gamma b h^2}{2}\right) \end{align}

The hydrostatic pressure distribution on the wall is shown below in red. Each red vector represents the force acting on each element $dA$ of the wall. We can see that this distribution of forces has a shape — a prism.

The 'volume' of this pressure prism, ${\rlap{V}-}$, is given by

\begin{align} {\rlap{V}-} = \frac{1}{2} \left( \gamma h \right) \left( h \right) \left( b \right) = \left( \frac{\gamma b h^2}{2} \right) \end{align}

so that the volume of the pressure prism is equivalent to the resultant force $F_R$. This should make intuitive sense since calculating the volume is the same as integrating over the pressure distribution.

To compute the vertical location where the resulting lumped force $F_R$ occurs we use

\begin{align} I_{yc} = \frac{b h^3}{12} \end{align}

and

\begin{align} y_R = \frac{I_{yc}}{y_c A} + y_c \end{align}

where $y_c = h/2$

which yields

\begin{align} y_R = \left (\frac{b h^3}{12} \right) \left( \frac{2}{h b h} \right) + \frac{h}{2} = \frac{b h^3}{6 b h^2} + \frac{h}{2} = \frac{h}{6} + \frac{3 h}{6} = \frac{2 h}{3} \end{align}

which is $\frac{2}{3}h$ measured from the free surface or $\frac{1}{3}h$ measured from the bottom.

Applied to a submerged surface¶

Sometimes the surface of interest is smaller than the entire vertical wall, such as an observation window, or access panel. The same method can be used with some care. Looking at the 3D model we can see that the orange vectors represent the pressure on our surface of interest.

The pressure prism in this region is not triangular as before, but is quadrilateral and is made up of a rectangular region and a triangular combined. The rectangular region accounts for the influence of the water above the surface of interest and the triangular region accounts for the variation across the height of the surface.

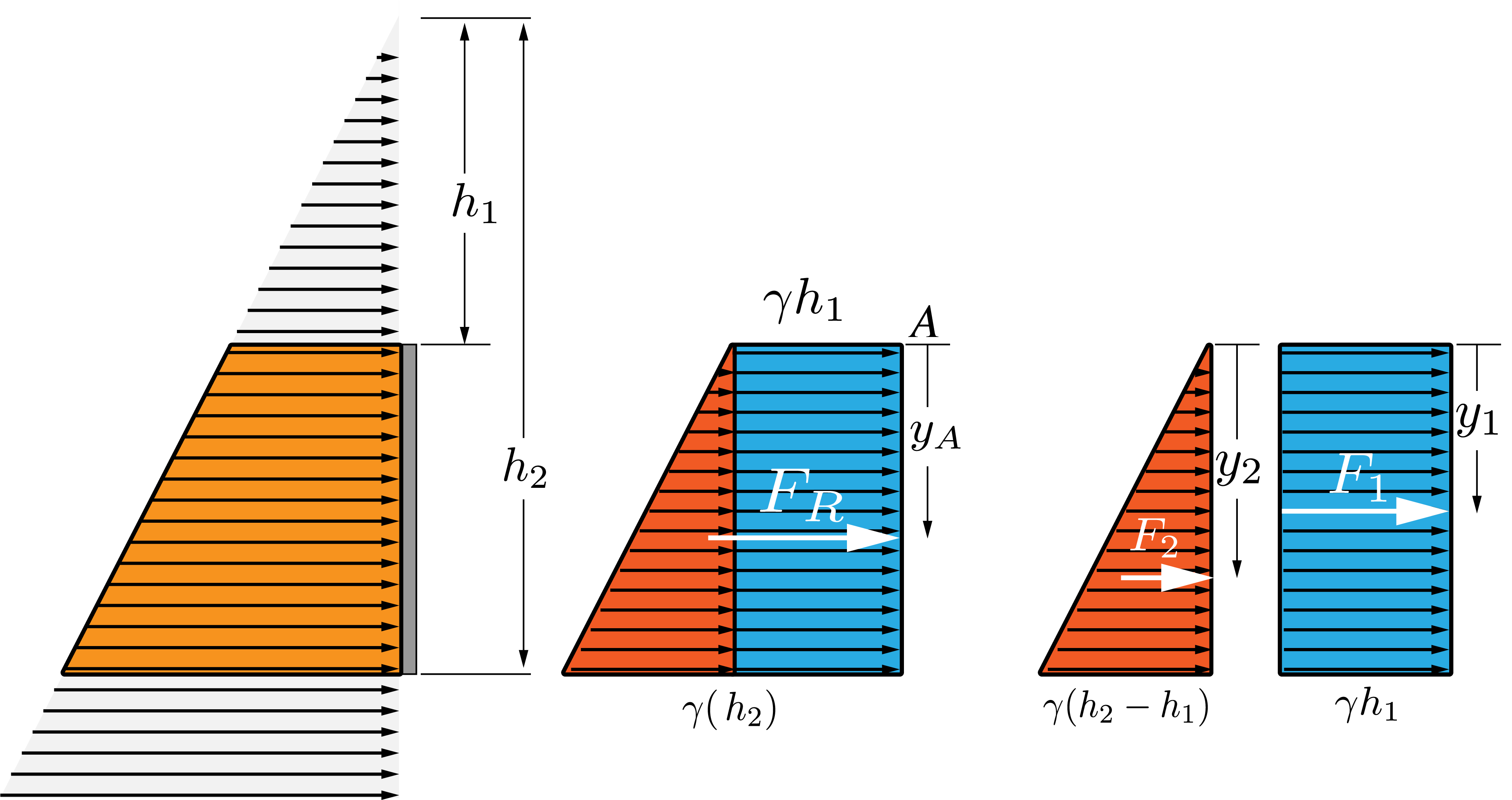
The resultant force is:

\begin{align} F_R = F_1 + F_2 \end{align}

The force due to the rectangular region is the pressure $\gamma h_1$ times the area $b(h_2 - h_1)$:

\begin{align} F_1 = \gamma h_1 b(h_2 - h_1) \end{align}

and the force due to the triangular region is obtained as above for a triangular pressure prism by computing the volume of the prism. Half the base by the height, times the width $b$.

\begin{align} F_2 = \gamma \frac{h_2 - h_1}{2} b(h_2 - h_1) \end{align}

To obtain $F_R$ we can take moments about the point A.

\begin{align} F_R y_A = F_1 y_1 + F_2 y_2 \end{align}

where

\begin{align} y_1 = \frac{(h_2 - h1)}{2},~~y2 = \frac{2}{3}(h_2 - h_1) \end{align}

Hydrostatic force on a curved surface¶

We can apply the same logic to curves surfaces by remembering that the pressure at any point is a function of the vertical depth only. We can define a region of fluid that encapsulates the curved region of the geometry shown below and consider the pressure acting on the flat sides of this region.

Let's use all the things we've learned to tackle this problem. We can find the force $F_1$ acting on the top of our region of fluid by using Pascal's law

\begin{align} F_1 = \gamma h \end{align}

where $h$ is the depth to this imaginary surface.

However the vertical force experienced at the bottom of the vessel is $F_1$ plus the weight $W$ of the fluid in our imaginary region of fluid.

\begin{align} F_V = F_1 + W \end{align}

Considering the side of our region of fluid we can observe that it is identical to our previous example with a submerged surface. The horizontal force $F_H$ is balanced by $F_2$.

\begin{align} F_H = F_2 \end{align}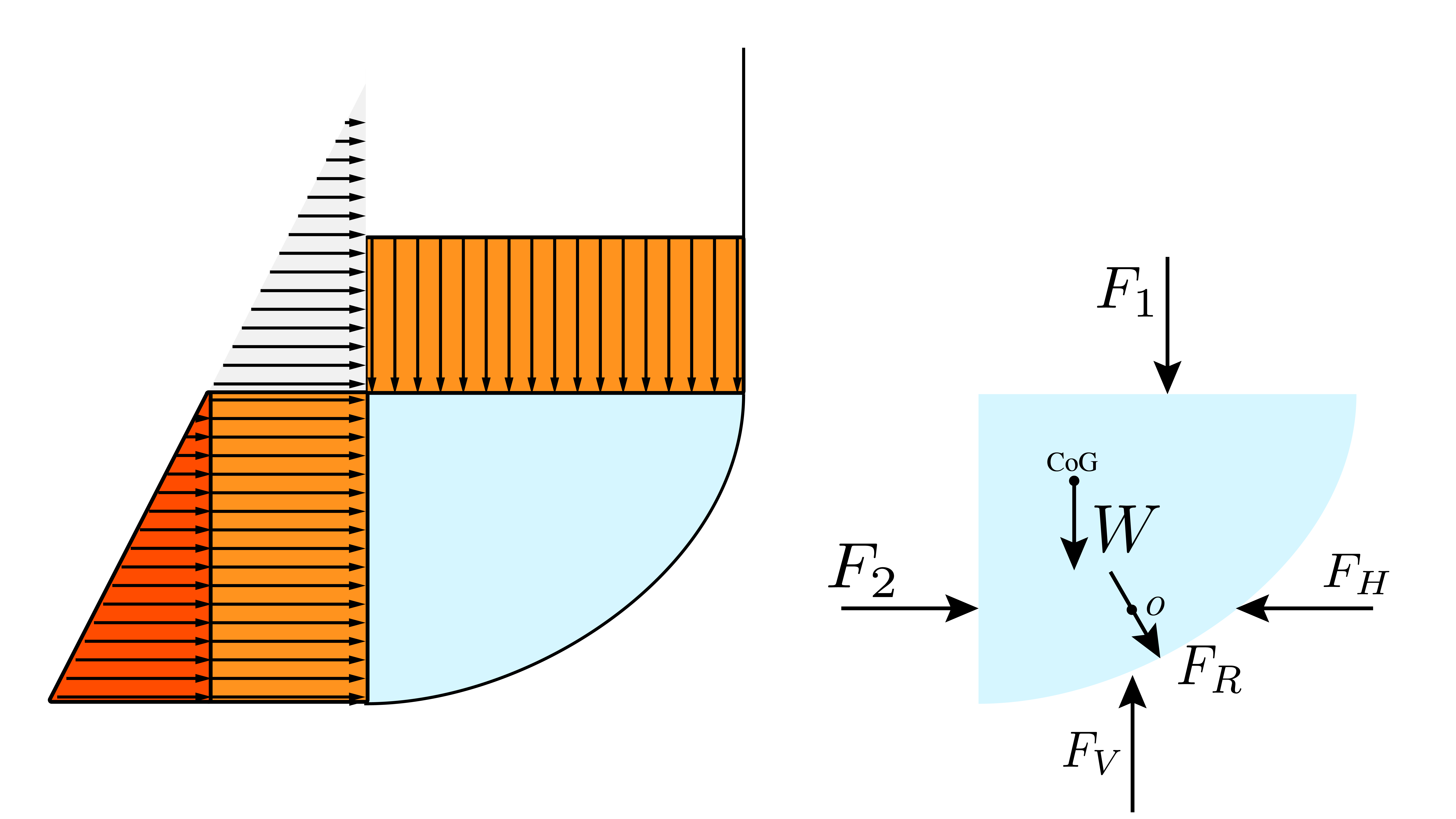

So we can calculate $F_H$ by considering the quadrilateral and triangular portions of the pressure prism and $F_V$ by considering the weight of the fluid. The resultant force $F_R$ is then:

\begin{align} F_R = \sqrt{F_H^2 + F_V^2} \end{align}

and it passes through the point $O$ which is vertically aligned with $F_H$ (and therefore $F_2$) and horizontally aligned with $F_V$, whose position is obtained by summing the moments of $F_1$ and $W$.

Buoyancy — Archimedes' principle¶

Many of us have heard the story of ancient Greek natural philosopher Archimedes sitting in the bath contemplating if the king's crown was made of gold and shouting "Eureka!" when he realised the solution.

When submerged in the bath Archimedes noticed that the water level would rise. He reasoned that the amount it rose would equal the volume of the submerged object. You may have reasoned something similar when considering the change in height $H$ of water in your siphon experiment. Archimedes could weigh the crown using a scales and the volume by observing the change in the water level and then determine the density of the crown.

But there is more to this story. When submerged some objects sink and some float. The fluid is exerting a force on the object in addition to its weight. It seems obvious that the density of the object plays a role. If we make our object more dense it will sink and if we make it less dense it will float upwards. This is how submarines operate; they fill their ballast tanks with water to sink deeper and with air to float upwards. The can achieve a neutral buoyancy when the average density of the vessel is just right.

Take a look at the 3D model below. There is an irregular shaped rock submerged under the water. Vectors show the hydrostatic pressure distribution around the rock. To make the analysis easier we consider the "bounding box" of the irregular rock. This is an imaginary box which the extremities of the rock fit into relative to our coordinate system. The volume of the bounding box is $(h_2 - h_1)A$.

We can simplify this scenario by considering the lumped forces $F1$, $F2$, $F3$ and $F4$ due to the hydrostatic effects and the weight of the water $W$ left over in the bounding box and finally the buoyancy force $F_B$.

Note that we are going to ignore the object itself. I've removed it from the 3D scene below.

This means we are only considering the effects of the fluid on the object.

If the rock of volume ${\rlap{V}-}$ has a different density to the liquid then it will either sink or float. The magnitude and direction of $F_B - W$ will determine this.

Therefore we need to account for the extra buoyancy force $F_B$ when summing the forces due only to the liquid. If we consider only the water in the bounding box

\begin{align} F_B = F_2 - F_1 - W \end{align}

Here $W$ is the weight of the fluid in the bounding box and is obtained by subtracting the volume of the rock from the volume of the bounding box.

\begin{align} W = \gamma((h_2-h1)A - {\rlap{V}-}) \end{align}

so that

\begin{align} F_B = \gamma(h_2 - h_1)A - \gamma((h_2 - h_1)A - {\rlap{V}-}) \end{align}

which reduces to:

\begin{align} F_B = \gamma {\rlap{V}-} \end{align}

$F_B$ is the force exerted by the liquid on the object. An equal but opposite force will be exerted by the object on the fluid via Newton's third law. This is a net upward force because the pressure and therefore the force exerted on the object increases with depth.

What is particularly interesting is that the buoyancy force is equal to the weight of water displaced.

An Example¶

A small research submersible has a volume of 25 $m^3$.

The density of seawater is approximately 1,025 $kg/m^3$.

The submersible's mass ($m_{sub}$) when its ballast tanks are empty is 16,000 kg.

The volume of the ballast tanks is 12 $m^3$.

Determine if the submarine will float, sink, or stay neutrally buoyant when its ballast tanks are:

a) Empty

b) Full

Part (a)¶

Weight of the submersible \begin{align} W_{empty} = m_{sub} \times g = 16,000 \times 9.81 = 156,960 N \end{align}

Calculate the specific weight for seawater: \begin{align} \gamma = \rho g = 1,025 \times 9.81 = 10,055.25 N/m^3 \end{align}

Calculate the Buoyancy Force

\begin{align} F_B = \gamma \times {\rlap{V}-} = 10,055.25 \times 25 = 251,381.25 N \end{align}\begin{align} F_B > W_{empty} \end{align}

When the ballast tanks are empty is is clear that the buoyancy force is much larger than the weight of the submersible and it will float to the surface.

Part (b)¶

When the ballast tanks are filled with seawater, the mass of the submarine increases by the weight of the seawater taken in.

\begin{align} W_{full} = m_{sub} \times g + \gamma {\rlap{V}-}_{tanks} = 16,000 \times 9.81 + 10,055.25 \times 12 = 277623 N \end{align}\begin{align} F_B < W_{full} \end{align}

With the ballast tanks full the weight of the submarine is greater than the buoyant force, so the submarine will sink.

Finishing up¶

We have looked at fluid statics in three separate notebooks covering hydrostatics, manometry and now hydrostatic forces exerted on various containers. You should work through Problem Set 1 on Brightspace or find some in a text book at the of the corresponding chapter.

References¶

1. Munson, B.R., Young, D.F., Okiishi, T.H. and Huebsch, W.W., 2010. "Fundamentals of Fluid Mechanics". Singapore: Wiley.